Índice:
Números y medidas en los primeros documentos escritos.
Investigación y ciencia. Número 91. Abril del 1984. Pàginas 68 a 76.
Ya a finales del cuarto milenio a. C., protosumerios y protoelamitas poseían sistemas de números y medidas bien desarrollados, entre los que se contaba un antecedente de nuestro propio sistema decimal.
Jöran Friberg.
Entre los primeros documentos escritos del mundo se encuentran unas inscripciones sobre tablillas de arcilla exhumadas en Irak e Irán, en particular en los yacimientos de dos grandes ciudades antiguas: la primitiva ciudad sumeria de Uruk y la antigua ciudad elamita de Susa. Las inscripciones, en su mayor parte cuentas y recibos de distintos tipos, se escribieron hacia finales del cuarto milenio a. C. y poco después. Tras muchas décadas de labor estudiosa, han podido identificarse todos los sistemas de números y medidas de estos textos «protoletrados». En ellas hallamos los antecedentes del sistema numeral sexagesimal sumerobabilónico posterior (que cuenta de 10 en 10 y de 60 en 60) y de nuestro propio sistema decimal (que cuenta sólo de 10 en 10). Encierran, además, un sistema de medidas de capacidad, no reconocido con anterioridad, utilizado en todas las cuentas concernientes a cebada, que en esta temprana fecha constituía tanto el cereal alimentario básico como la moneda.
El lector que guste saber sobre los sistemas numeral y de medidas protoletrados tendrá que seguirme en un viaje de dos direcciones. Viajaremos hacia atrás en el tiempo, con respecto a la documentación histórica, y hacia adelante, desde el pasado hacia el presente, por lo que a los estudiosos que han investigado las tablillas antiguas respecta. La razón de que debamos hacerlo así estriba en que las tablillas más antiguas yacían enterradas a mayor profundidad y fueron, por tanto, las últimas en rescatarse y ser accesibles para su estudio. Las tablillas más antiguas eran también las de más difícil interpretación.
Tomemos por punto de partida la costera isla griega de Cos, a unos 32 kilómetros al noroeste de Rodas. Allí, hacia el 340 a. c., el fundador de una escuela de astrología, un babilonio llamado Beroso, escribió una historia de su tierra de origen. En dicha historia contaba a sus lectores griegos que los numerales sossos (60), neros (600) y saros (3600) ocupaban un lugar especial en la aritmética y astronomía babilónicas. Nada más se supo sobre numerales y medidas babilónicas en los siguientes 2200 años. En 1855, Sir Henry Rawlinson, uno de los pioneros del desciframiento de la escritura cuneiforme, publicó un resumen de los numerales cuneiformes inscritos en una pequeña tablilla de arcilla hallada en el yacimiento de la antigua ciudad mesopotámica de Larsa. Entre otras cosas, Rawlinson se dio cuenta de que las dos últimas líneas de la tablilla establecían en efecto que «58 1 es el cuadrado de 59» y que «1 es el cuadrado de 1». Concluyó que la tablilla era la parte final de una tabla dé raíces cuadradas, que comenzaba con el cuadrado de 49 (igual a 2401, o 40 x 60 + 1) Y finalizaba con el cuadrado de 60 (igual a 3600 o 60 x 60). Por supuesto que su interpretación sólo era posible si se suponía que los numerales 60 y 60 x 60 estaban ambos representados por el mismo símbolo, esto es, el del número 1.
Rawlinson sacó la conclusión de que los babilonios habían operado con una notación numérica sexagesimal de una naturaleza cuasiposicional; en otras palabras, una notación numérica en la que el símbolo para 1 representaba también las potencias de 60 y, el símbolo 10, 10 veces las potencias de 60. Llegó a la conclusión adicional de que los babilonios no tenían ningún signo especial para representar el cero.
Resulta necesario considerar aquí sucintamente los méritos relativos de los sistemas numerales de bases diferentes. Comencemos por el denominado sistema métrico, que es en realidad una familia de sistemas interrelacionados de unidades para varios tipos de medidas. El sistema métrico debe su aceptación general a su sencillez estructural y al hecho de que está construido para adecuarse a la base 10, o decimal, un sistema empleado hoy para todo tipo de cómputo ordinario. Desde su creación en Francia entre los productos de la Revolución Francesa, se ha difundido gradualmente por todo el mundo.
El propio lapso temporal que le ha costado al sistema métrico hacerse con una aceptación general constituye la prueba de cuán difícil resulta eliminar otros sistemas «consuetudinarios» de pesos y medidas. Los ejemplos ingleses de dichos sistemas incluyen las secuencias mile, furlong, chain, rod, yard, foot e inch (o las tradicionales castellanas de milla, legua, braza, vara, pie y pulgada) para las medidas de longitud, barrel, bushel, peck, quart y pint (fanega, celemín, almud, cuartera o cuartillo) para las medidas de áridos, y ton, hundredweight, pound y ounce (tonelada, quintal, arroba, libra y onza) para las medidas de peso. Por esta cuestión, incluso el sistema métrico, en su forma no científica, ha llegado a incorporar sistemas no decimales: el año de 12 meses, el día de 24 horas, la hora de 60 minutos, el minuto de 60 segundos, como unidades de tiempo, y la circunferencia de 360 grados, con sus subdivisiones de grado de 60 minutos y minuto de 60 segundos, como unidades de medición de ángulos. Estas medidas ordinarias pueden ser retrotraídas hasta la astronomía griega clásica y aún más allá, hasta el uso general de numerales sexagesimales para el cálculo en Babilonia y Sumeria. Muchos otros sistemas habituales de pesas y medidas estaban condenados, sin embargo, a ser sustituidos por el sistema métrico decimal, debido a que no se adecuaban suficientemente al sistema numérico decimal adoptado de un modo general.
Con todo, la pervivencia de algunos sistemas ordinarios ha sido en parte responsabilidad del propio sistema numérico decimal. El sistema decimal encierra la debilidad de que su base de 10 es, en realidad, demasiado pequeña. Esto quedará más claro en cuanto aporte unos ejemplos adicionales de cálculos dentro del marco del sistema sexagesimal, con su base mayor: 60 = 3 x 4 x 5 (en oposición a 10 = 2 x 5). Como se podrá ver, el sistema de base 60 permitió que los predecesores protoletrados de los sumerios construyeran una familia de sistemas métricos perfectamente relacionados entre sí, con secuencias de unidades canónicas de aparición natural de fácil manejo en los cálculos.
Hallar la interpretación correcta del sistema de notaciones cuneiformes que sirven para representar números sexagesimales (o de base 60), resultó relativamente fácil. Más difícil resultó entender cómo estaban construidos los distintos sistemas de medidas que aparecen en numerosas inscripciones cuneiformes. Algunas claves decisivas las ofrecieron ciertos tipos de tablillas que los estudiosos interpretan como textos escolares.
La copia de textos canónicos constituía parte esencial de la carrera escolar en la época del Babilónico Antiguo o Paleobabilónico (del 1900 al 1500 a. C.). Muchos de estos textos eran listas y tablas: listas de nombres geográficos, listas de nombres de aves y peces, listas de palabras en dos lenguas, tablas gramaticales para el estudio de la difícil lengua sumeria, etcétera. También se copiaban tablas matemáticas y tablas de medidas. Al hacer este tipo de copia, un estudiante se formaba en la escritura cuneiforme y al mismo tiempo reunía una pequeña biblioteca personal de tablillas.
El primer ejemplo de una tabla de medidas descrito en una publicación científica fue una tablilla fragmentaria descubierta también en Larsa. La tabla fue investigada en 1872, por George Smith, notable estudioso del cuneiforme, pero su significado no se comprendió enteramente hasta mucho más tarde. En el lado izquierdo de cada columna de la tablilla hay una secuencia, dispuesta de un modo sistemático, de mediciones de longitud, expresadas en unidades al uso. Estas unidades son, de menor a mayor, el she (un grano), el shu-si (un dedo), el kush (un codo) y así sucesivamente hasta el beru, equivalente a 30 x 60 x 12 (6 x 602), o 21.600 codos. En la parte derecha de cada columna aparecen las mismas mediciones de longitud expresadas en múltiplos de codos en notación sexagesimal. Por ejemplo, la línea de la parte inferior derecha identificada como a en la reproducción de una tablilla que aparece en la figura 4 reza «Dos beru [equivalen a] 12». Debería señalarse que beru representa la pronunciación babilónica del símbolo para la palabra sumeria danna (escrita normalmente como kas-gid, que significa «camino largo»). No obstante, el 12 no representa 12 codos, sino la suma mucho mayor de 12 x 602 codos. Con un codo que equivalga a medio metro de longitud aproximadamente, la longitud del beru era superior a los 10 kilómetros.
Cuando se identificó otro fragmento de la misma tablilla poco después de que se hallara el primero, se vio que contenía otra tabla metrológica del mismo tipo que la primera, excepto en que, en este caso, la parte derecha de cada columna tenía que ver con múltiplos de un nindan (equivalente a 12 codos) en la notación sexagesimal. Sólo mucho más tarde el estudio de los textos matemáticos babilónicos que atañen al cálculo de volúmenes puso de manifiesto que, mientras que el codo constituía la unidad básica para las medidas verticales, el nindan era la unidad para las mediciones horizontales. De aquí que la menor unidad de superficie sumerobabilónica, el shar, fuera un nindan cuadrado. Del mismo modo, la menor unidad de volumen, llamada también shar, era el espacio contenido por un área de base de un nindan cuadrado que tuviera lados de un codo de alto. Esta serie aparentemente peculiar de unidades era realmente bastante práctica, pues evitaba por lo general la necesidad de contar con fracciones menudas de una unidad de volumen.
Estas dos tablas metrológicas constituyen un testimonio elocuente de la perfección con la que el sistema de mediciones de longitud sumerobabilónico se adaptaba al sistema numérico sexagesimal. Considérense las reglas de conversión para las unidades del sistema métrico de longitud. Seis she equivalen a un shu-si, 30 shu-si equivalen a un kush, 12 kush equivalen a un nindan, 60 nindan equivalen a un USH y 30 USH equivalen a un danna (o beru).
La información contenida en esta secuencia de reglas de conversión puede condensarse del siguiente modo: los «factores de conversión» para el sistema lineal babilónico son 6, 30, 12, 60 y 30. Véase que cada uno de dichos factores es también un factor numérico del sistema numeral sexagesimal. A modo de comparación, la secuencia anglosajona de la pulgada a la milla da los factores de conversión siguientes: 12, 3, 5½, 4, 10 y 8. Cualesquiera que sean los orígenes de los factores de este sistema ordinario, está claro que no se adaptan en modo alguno a nuestro sistema numérico decimal.
Las excavaciones de Mesopotamia no sólo han proporcionado textos de interés matemático, como los procedentes de Larsa, sino también «textos con problemas», que aún son más sustanciosos. Ya en 1900 el Museo Británico reproducía dos grandes tablillas del Babilónico Antiguo que presentaban problemas matemáticos variados. Su terminología matemática era difícil e inusual, y así pasaron unos 30 años antes de que se interpretaran la mayoría de los problemas y se entendieran plenamente. En la actualidad son accesibles para su estudio un gran número de textos con problemas matemáticos del Babilónico Antiguo. Sin embargo, extendernos en los mismos quedaría fuera del ámbito de esta exploración de sus orígenes. Pasemos por tanto a otros textos publicados a principios de siglo.
Entre 1889 y 1900, una expedición estadounidense llevó a cabo una importante excavación en Nippur, uno de los yacimientos más extensos e importantes de Mesopotamia. En 1906, Herman V. Hilprecht, de la Universidad de Pennsylvania, informó de algunos de los resultados de la expedición en un volumen que incluía reproducciones de varios textos matemáticos y rnetrológicos importantes del Babilónico Antiguo y un texto de problemas escrito en sumerio. (Sólo hace un año que pude mostrar que este texto de problemas contiene una serie de problemas geométricos tridimensionales resueltos mediante reducción a ecuaciones cúbicas y obtención de raíces cúbicas).
Los textos metrológicos del Babilónico Antiguo publicados por Hilprecht incluían tablas de conversión sexagesimal para varios tipos de medidas y listas de medidas de menor a mayor. Puede suponerse que dichas listas servían para enseñar tanto la estructura de los sistemas de medidas surnerobabilónicos como la forma de los signos numerales y demás signos que pertenecían a cada sistema.
La publicación de Hilprecht demostró una semejanza palmaria entre las tablas del Babilónico Antiguo, de un lado, y vocabularios y listas léxicas o gramáticas sumerobabilónicas, del otro. Desde entonces se han exhumado un buen número de textos correspondientes a esas categorías. Los más antiguos de los mismos los constituyen unas pocas listas léxicas protoletradas que datan de finales del cuarto milenio a. C. Las tablas matemáticas más antiguas son medio milenio más recientes.
Si proseguimos ahora nuestro viaje hacia atrás en el tiempo, hasta los comienzos del tercer milenio a. c., llegamos al período sumerio conocido como Ur III (2050-1950 a. C.), que precedió inmediatamente al período del Babilónico Antiguo. Se conoce gran cantidad de textos de Ur III, en su mayoría de carácter administrativo o económico. En ellos se empleaba, como norma, una notación no posicional para los números sexagesimales, con signos independientes para 1, 60 Y 602, para 10, 10 x 60, Y 10 X 602, y así sucesivamente. Con este tipo de notación no posicional no había necesidad de un signo especial para el cero.
Solamente unos pocos de entre los numerosos textos de Ur III son de algún interés por su contenido matemático o metrológico. Mencionaré aquí precisamente un reducido grupo de éstos, que se ocupan de cálculos de la cantidad de simiente necesaria para sembrar campos de unas dimensiones dadas, cuando el espaciamiento de los surcos se daba como N surcos por nindan. Las copias conservadas de una especie de Almanaque del Granjero sumerio indican que se depositaban regularmente en el surco los granos a intervalos de dos dedos (shu-si), esto es, a razón de 180 granos (equivalentes a una unidad de capacidad denominada shekel [siclo]) por nindan. Cuando, como por lo general era el caso, N era igual a 10, esta razón podía expresarse justamente como un gur (la unidad mayor de capacidad) por bur (la unidad mayor de superficie). Este ejemplo, en el que un grano por dos dedos equivale a un siclo por nindan o a un gur por bur, muestra de qué modo las distintas unidades de medida sumerobabilónicas aparecían perfectamente interrelacionadas a pesar de su aparente complejidad.
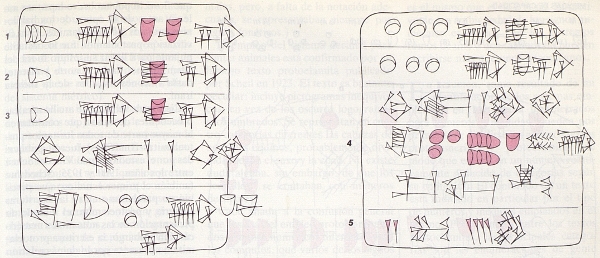
El dominio sumerio en Mesopotamia durante el tercer milenio se rompió por un breve interludio semítico, que comienza con el reinado de Sargón de Acad (2350-2300 a. C.). La existencia de una actividad matemática en el período de Sargón y de sus sucesores, que difícilmente puede ponerse en tela de juicio, aparece confirmada por un puñado de pequeñas tablillas que registran ejercicios geométricos sencillos, pero en modo alguno triviales. El período sargónico es ilustrado aquí con una tablilla procedente de la ciudad de Umma y que presenta una cuenta de ofrendas religiosas, diarias y mensuales de cerveza. Su texto incluye interesantes cálculos metrológicos. Muestra asimismo con claridad que los símbolos numéricos podían escribirse en dos formas: como signos cuneiformes, inscritos con el extremo en forma de cuña de un cálamo, o como signos circulares realizados con el extremo romo del mismo.
Pocos textos matemáticos más se conocen del período sumerio presargónica y del precedente período de Fara, el Sumerio Antiguo o Paleosumerio, de mediados del tercer milenio a. C. El texto metrológico más antiguo que se conoce es del período de Fara, y enumera las áreas de grandes campos cuadrados hasta incluir un campo de (10 x 60 nindan)2, Recientemente he tenido la oportunidad de identificar otro texto de Fara como un ejercicio geométrico relacionado con el anterior. Otros dos textos matemáticos del período de Fara son bien conocidos. Ambos tratan del mismo problema de división con grandes cifras sexagesimales en juego. Aunque esta pequeña muestra de textos no permite alcanzar conclusiones trascendentales, parece claro que los primitivos maestros sumerios, cuya tarea parece haber sido la instrucción en lo que podría denominarse matemáticas elementales aplicadas, sobresalían realmente en la operación con problemas bastante abstractos que encerraban números o medidas muy elevadas o reducidas, con algoritmos para la multiplicación o la división, con cálculos de superficies basados en tablas de áreas cuadradas y otras cuestiones por el estilo. Como podremos ver, esta predilección por operar con cifras grandes y menudas imaginarias puede retrotraerse hasta el período protoletrado.
¿Cómo se desarrollaron los sistemas matemático y metrológico sumerios? La presentación de los datos principales entraña otro paso hacia atrás, hacia los comienzos del tercer milenio a. C. En 1928, Stephen H. Langdon, de la Universidad de Oxford, publicó una colección de unos 200 textos que habían sido excavados unos pocos años antes en el pequeño yacimiento de Jemdet Nasr, en el Irak. (La colección de Jemdet Nasr está en la actualidad dividida entre el Museo de Ashmole de Oxford y el Museo Iraquí de Bagdad.) Las nuevas inscripciones estaban escritas en una escritura pictográfica arcaica, claro antecedente de la cuneiforme sumeria. No obstante, muchos de los signos de estos textos arcaicos ya no se utilizaban en la época en que se concibieron los textos cuneiformes del período de Fara, del Sumerio Antiguo. Por dicha razón aún hoy no se conoce la lectura correcta de muchos signos de las inscripciones «protosumerias» de Jemdet Nasr y los textos siguen siendo más o menos ininteligibles. Tampoco está totalmente claro que la lengua de las tablillas de Jemdet Nasr sea sumerio, por lo que precisamente hago referencia a las mismas como protosumerias. Sin embargo, los números que aparecen en dichos textos, realizados normalmente con el extremo redondeado de los estilos, son siempre de fácil identificación. Se reconoció de inmediato que las notaciones numéricas de las tablillas de Jemdet Nasr presentaban una íntima relación con los de otras tablillas aún más enigmáticas procedentes del Irán. Estas tablillas se denominan, por razones similares, protoelamitas, y son más o menos de idéntica fecha. Volveremos sobre ellas más adelante.
En 1936, menos de una década después de la publicación de las tablillas de Jemdet Nasr por Langdon, el estudioso alemán Adam Falkenstein publicó otra colección de tablillas protosumerias, claramente más antiguas y en cierto modo más primitivas que las de Jemdet Nasr. La colección de Falkenstein incluía 600 inscripciones, pero éstas representaban solamente una pequeña parte del total recuperado por una expedición alemana que había excavado en el yacimiento de la importante ciudad mesopotámica de Uruk, en los primeros años de la década de 1930. La mayor parte de las tablillas publicadas procedían del Nivel IV de dicho yacimiento. El resto de la colección (ahora en Berlín) se publicará en un futuro cercano.
Tres textos de Jemdet Nasr que tratan de cálculos de superficies fueron interpretados en 1930 por el estudioso francés Francois-Maurice Allotte de la Fuye, quien demostró que el sistema numeral sexagesimal y el sistema sumerio de medidas de superficie se empleaban también en estas inscripciones protosumerias. Con esta excepción, no obstante, las notaciones protosumerias para números y medidas continuaron comprendiéndose poco. Se suponía por lo general, empero, que, junto al sistema sexagesimal sumerio, los escribas primitivos recurrían a un sistema numeral decimal (o «centesimal»), tomado en préstamo posiblemente del protoelamita. Se suponía igualmente, por razones poco fundadas, que en los textos cerealísticos protosumerios (caracterizados por el signo she, que significa grano) la principal unidad de capacidad era un gur que contenía 300 sila (o 30 ban), al igual que en los textos de carácter cerealístico del período bien posterior de Ur III.
En 1978 pude demostrar la falsedad de dichas suposiciones al probar que en ambos tipos de textos cerealísticos protoletrados, protosumerios y protoelamitas, el signo numérico leído invariablemente por los estudiosos como 10 muy probablemente tuviera también el valor de 6. En efecto, incluso en un mismo texto el mismo signo numérico puede leerse como 10 o como 6, según el contexto.
Esta nueva perspectiva posibilitó de inmediato la comprensión de los cálculos de cientos de textos con medidas de capacidad protosumerios y protoelamitas, textos que no había sido posible analizar anteriormente. Al establecer paralelos entre determinadas clases de textos protoletrados y sus correlatos sumerios pude determinar, además, al menos de una forma aproximada, el valor absoluto de la principal unidad de capacidad protoletrada, que resultó ser poco más o menos un ban sumerio (aproximadamente 10 litros) y no el pretendido 30 ban.
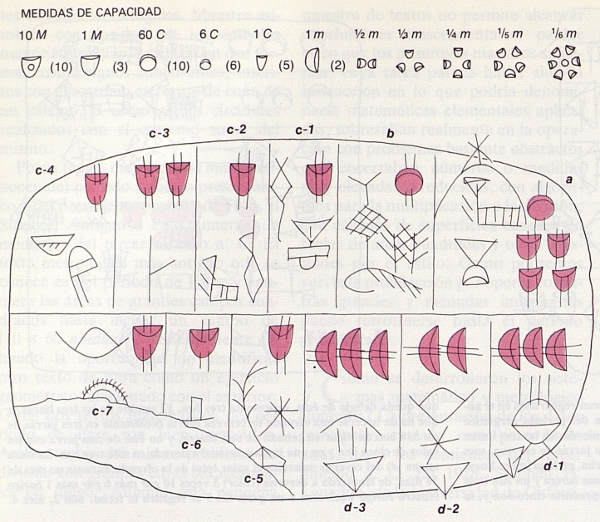
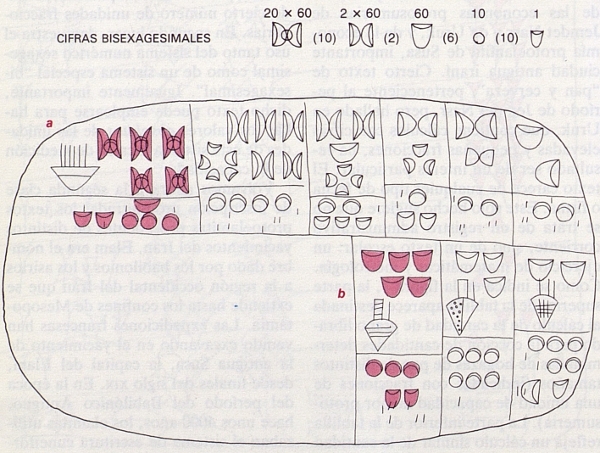
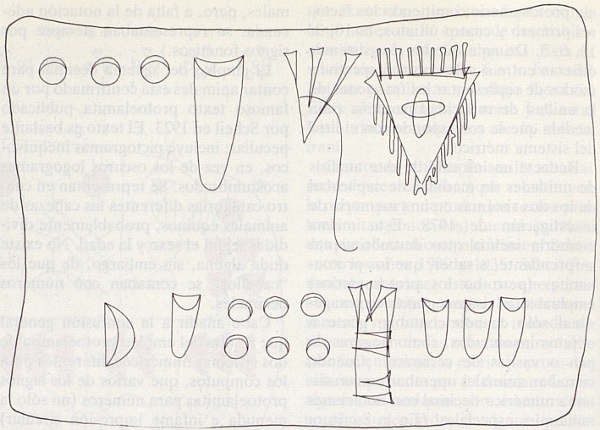
Gracias a estos progresos, pueden en la actualidad comenzar a determinarse correctamente la escala y carácter de las economías protosumerias de Jemdet Nasr y de Uruk, y de la economía protoelamita de Susa, importante ciudad antigua iraní. Cierto texto de «pan y cerveza», perteneciente al período de Jemdet Nasr, pero hallado en Uruk, que contiene cálculos con cifras elevadas y pequeñas fracciones, ha resultado ser de un interés particular. El texto carece de cualquier tipo de fecha o firma. Este solo hecho sugiere que no se trata de un registro administrativo corriente, sino de un texto escolar: un ejercicio de matemáticas y metrología. Como se indica en la figura 7, la parte superior de la tablilla aparece destinada al cálculo de la cantidad de grano librado para la cocción de cantidades determinadas de hogazas de pan de distintos tamaños (indicadas con fracciones de una unidad de capacidad menor protosumeria). La parte inferior de la tablilla refleja un cálculo similar de la cantidad de grano librado para la elaboración de dos jarras de cerveza fuerte, tres jarras de cerveza de grado medio y cinco jarras de cerveza ligera. Las diferentes gradaciones de los tres lotes de cerveza quedan manifestadas por las diferentes cantidades de grano por jarra de los tres ejemplos.
Este preciso ejemplo de un texto protosumerio del tipo de Jemdet Nasr es importante por varias razones. En primer lugar, establece sin lugar a dudas los valores relativos de algunas unidades del sistema protosumerio que servían para medir la capacidad, incluido cierto número de unidades fraccionarias. En segundo lugar, demuestra el uso tanto del sistema numérico sexagesimal como de un sistema especial «bisexagesimal». Igualmente importante, dicho texto puede emplearse para hallar los valores absolutos de las unidades de este sistema arcaico de medición de la capacidad.
Volvamos ahora a la segunda clase de inscripción protoletrada, los textos protoelamitas procedentes de distintos yacimientos del Irán. Elam era el nombre dado por los babilonios y los asirios a la región occidental del Irán que se extiende hasta los confines de Mesopotamia. Las expediciones francesas han venido excavando en el yacimiento de la antigua Susa, la capital del Elam, desde finales del siglo XIX. En la época del período del Babilónico Antiguo, hace unos 4000 años, los elamitas utilizaban el sistema de escritura cuneiforme sumerobabilónico. Las excavaciones de Susa y de otros lugares del Irán han revelado, no obstante, la existencia de una civilización iraní anterior que utilizaba una escritura no cuneiforme y que floreció por un breve lapso un milenio antes de la época de los babilonios antiguos y de los elamitas. Esta civilización protoelamita fue lo bastante pujante para llevar su influjo fuera del Elam mismo, hacia el norte y el este, hasta rincones alejados de la meseta iraní.
Cientos de tablillas de arcilla arcaicas procedentes de Susa (que constituyen la mayor parte de todos los textos protoelamitas conocidos) fueron publicadas por el estudioso galo Vincent Scheil entre los años 1900 y 1935. Scheil fue también el primer estudioso que percibió un paralelismo entre las escrituras sumeria y protoelamita: el método de presentación de las notaciones numéricas. Sin embargo, la escritura protoelamita no presenta por lo demás relación alguna con cualquier otra escritura conocida. Su repertorio de signos, que representan las palabras o sílabas de una lengua desconocida, es de poca ayuda al ser abstracto, y no pictográfico, circunstancia esta que podría parecer que hace la interpretación de las partes no numéricas de los textos protoelamitas virtualmente imposible.
Los primeros intentos de Scheil por entender la naturaleza de los sistemas numerales de sus textos protoelamitas no fueron, desgraciadamente, afortunados. Fue incapaz de reconocer que un solo signo -una pequeña impresión circular- no tiene siempre necesariamente el valor numérico de 10. De este modo llegó por cierto tiempo a la conclusión de que los protoelamitas, al igual que los egipcios antiguos, operaban con un sistema numérico decimal en todas sus cuentas y cálculos. Más tarde, empero, encontró que algunos textos protoelamitas presentan un signo especial para 60. También identificó Scheil una serie de notaciones fraccionarias y llegó a identificar correctamente el logograma protoelamita para «grano» o quizá «medida de áridos».
Un texto protoelamina con un ejercicio matemático-metrológico, publicado por Scheil en 1935, trata de la suma de una larga serie de cifras de muchos dígitos que representan medidas de capacidad. Este texto particular proporciona una confirmación excelente de mi propio análisis de la estructura de las unidades protoelamitas para medir la capacidad. El sistema estaba construido claramente para adecuarse al sistema numérico sexagesimal (o bisexagesimal); posee la siguiente secuencia de factores de conversión de una unidad a la siguiente: 6, 10, 3, 10, 6, 5, 2, 3, 2, 2. La serie correspondiente de factores de conversión para las unidades del sistema protosumerio, omitiendo los factores primero y cuatro últimos, es 10, 3, 10, 6, 5. De aquí que los dos sistemas difieran entre sí sólo en sus respectivos modos de representar las fracciones de la unidad de capacidad pequeña (una medida que se corresponde con el litro del sistema métrico).
Redacté un informe de este análisis de unidades de medidas de capacidad de los dos sistemas en una memoria de investigación de 1978. Esta misma memoria incluía otro descubrimiento sorprendente, a saber, que los protoelamitas (pero no los protosumerios) empleaban el sistema numérico sexagesimal sólo cuando contaban gente u objetos inanimados, como hogazas de pan o vasijas de cerámica. ¡Cuando contaban animales operaban con un sistema numérico decimal con notaciones numerales especiales! (En la escritura cuneiforme sumero-babilónica se empleaban ocasionalmente números decimales, pero, a falta de la notación adecuada, se representaban siempre por signos fonéticos).
El empleo del sistema decimal para contar animales está confirmado por un famoso texto protoelamita publicado por Scheil en 1923. El texto es bastante peculiar: incluye pictogramas inequívocos, en vez de los oscuros logogramas acostumbrados. Se representan en cuatro categorías diferentes las cabezas de animales equinos, probablemente divididas según el sexo y la edad. No existe duda alguna, sin embargo, de que los «caballos» se contaban con números decimales.
Cabe añadir a la confusión general que resulta del empleo protoelamita de dos sistemas numéricos diferentes para los cómputos, que varios de los signos protoelamitas para números (no sólo la menuda e infame impresión circular) poseen valores diferentes según el contexto. Por ejemplo, el signo para 1000 es el mismo que el de 2 x 60. El motivo de esa ambigüedad de los signos numerales es obvio: con los extremos romos de uno o dos cálamos no pueden escribirse más que unos pocos signos.
En resumen, como resultado de mi identificación de los sistemas empleados en los textos protoletrados para números y medidas, pueden por primera vez dividirse los arcaicos textos protosumerios y protoelamitas de modo que entren en un número relativamente reducido de categorías según su contenido. El contenido de un texto está indicado en particular por el tipo de números y medidas empleados en el mismo. Por ejemplo, entre los textos protoelamitas, las principales categorías son las enumeraciones de gente (cómputo sexagesimal), cálculos de cereal librado en raciones para gente (números de capacidad y números sexagesimales) o para animales (números de capacidad y números decimales), textos de pan y cerveza (números de capacidad y números sexagesimales), cuentas de grupos de animales (números decimales), cuentas de hogazas de pan o vasijas cerámicas (números sexagesimales) y cuentas de grandes cantidades de cereal libradas de -o enviadas a- los almacenes, en un caso durante una «semana» de cinco días (número de capacidad). Pueden encontrarse otras categorías en los textos protosumerios: cálculos de superficies (números de superficie y números sexagesimales) y en un único ejemplo de un texto de sementera (números de superficie y números de capacidad).
Queda mucho por hacer hasta que las colecciones de textos protoletrados, publicados o sin publicar aún, nos ofrezcan toda la información que encierran. Sin embargo, se han realizado tantos avances, en particular en la última década, que ya puede bosquejarse un esquema plausible del desarrollo de la numeración y la metrología en el Asia sudoccidental desde la época prehistórica hasta la babilónica tardía.
En particular se sabe en la actualidad, gracias a la obra de Denise Schmandt-Besserat1, de la Universidad de Texas en Austin, que una variedad de «fichas» de arcilla sirvieron en dicha región, desde el milenio noveno a. C. hasta finales del cuarto, para designar números, medidas y quizá categorías de objetos. También se sabe que el empleo de fichas sueltas se complementó, a finales del cuarto milenio, con el recurso de incluir símbolos escogidos en una especie de sobres protectores de arcilla. Los sobres parecen haber inspirado a su vez la invención de las «tablillas impresas» (el término hace referencia a tablillas de arcilla con notaciones numéricas y normalmente improntas de cilindros-sello, pero carentes de todo signo abstracto o logograma).
La similitud de la forma de los signos numéricos de las tablillas impresas y la forma de las fichas de arcilla anteriores muestra una continuidad de las representaciones de números y medidas desde la época del nacimiento de las ciudades-estado en el Asia sudoccidental hasta, remontándonos en el tiempo, el Neolítico Temprano, hace 10.000 años. Además, el hecho de que las notaciones para unidades que pertenecen a los distintos sistemas de números y medidas protoletrados aparezcan también con claridad en algunas tablillas impresas muestra una continuidad en las representaciones de los números y medidas desde finales del cuarto milenio a. C. en adelante, sin solución de continuidad, hasta el período del Babilónico Antiguo, que se sitúa unos 2000 años más tarde. Y, como hemos visto, nuestro propio sistema decimal, así como nuestra forma de dividir el tiempo en horas, minutos y segundos, es un reflejo de esa misma continuidad hasta el día de hoy.